Comunicación presentada al VI Congreso Smart Grids
Autores
- Dr. Jesús Besada Juez, Departamento de Ingeniería, Qwi Tecnologías de la Información
- Ana González Bordagaray, Control Systems, I-DE Redes eléctricas Inteligentes, Grupo Iberdrola
- Jesús Javier Ferro Vázquez, Sistemas de Control, I-DE Redes eléctricas Inteligentes, Grupo Iberdrola
- Gustavo Plaza González, Departamento de Ingeniería, Qwi Tecnologías de la Información
Resumen
El control y monitorización de sistemas de potencia requiere procesar grandes cantidades de información en tiempo real de múltiples fuentes de manera precisa y fiable. Los centros de control modernos utilizan algoritmia avanzada para dicha tarea, donde el estimador de estados es uno de los más populares. Se presenta un algoritmo novedoso que consigue todos los beneficios de reducir la dimensión de la matriz de ganancias, pero sin los inconvenientes de los enfoques tradicionales como el fast decoupled. Para ello se propone resolver el problema del estimador de estado en el dominio de los números complejos en vez de en el de los números reales. La mejora en velocidad y recursos del nuevo algoritmo lo sitúa en un puesto privilegiado para afrontar los nuevos retos de las redes Smart Grids, con cientos de miles de medidas obtenidas en tiempo real y escenarios cada vez más complejos de operación.
Palabras clave
Estimador de Estados, WLS, Matriz de Ganancias, Fast Decoupled, Dominio Complejo, Smart Grid
Introducción
La estimación de estados es el proceso de inferir los mejores valores posibles de las variables de estados del sistema usando un número limitado de medidas y la información topológica de la red. Las principales virtudes que se buscan son: rapidez de cálculo, una alta precisión y capacidad para detectar y corregir de forma automática las medidas anómalas [3].
De las diferentes estrategias utilizadas, los algoritmos de mínimos cuadrados ponderados [6] (weighted least squares -WLS-) son con mucho, los más populares y se invierte una gran cantidad de esfuerzo e investigación en mejorar dichos algoritmos [1][2].
La principal diferencia entre las diferentes propuestas utilizadas es el tipo de variable de estado que se utiliza [4]. Donde una vez elegida la variable de estado, el problema se formula siempre o en coordenadas polares o en coordenadas cartesianas [5]. Típicamente para redes de transmisión (aunque igual de válido para redes de distribución) se utiliza la magnitud y el ángulo de la tensión en los buses como variable de estado, en este caso, las entradas en la matriz Jacobiana y la factorización de la matriz de ganancia deben ser recalculadas en cada iteración. El siguiente apartado introduce la formulación de este problema.
Estimador de estados
El estimador de estados resuelve el conocido problema de optimización ponderada por mínimos cuadrados (WLS), que busca minimizar el error de las medidas disponibles:
![]()
Donde z es el vector de medias de dimensión m, y h es el vector de las estimaciones obtenidas por las ecuaciones no lineales de potencia dependiente del vector de estados de dimensión n, donde n, formulado en coordenadas polares tiene una dimensión igual al doble de buses del sistema.
Por lo tanto, se define la siguiente función objetivo a minimizar:
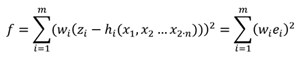
Donde w es el vector de pesos de las medidas, que típicamente toma el valor de la inversa de la desviación estándar del aparato de medida utilizado, es decir, .
Para encontrar el mínimo de la función objetivo, se calculan las derivadas parciales y se igualan a cero:
![]()
Donde H es la matriz Jacobiana de derivadas parciales de dimensión:
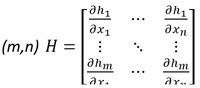
y W es la matriz diagonal de pesos de dimensión (m,m) y e es el vector de errores de dimensión m.
La ecuación (1) contiene m ecuaciones no lineales dependientes de n variables que no pueden resolverse de forma directa, lo que obliga a utilizar un proceso iterativo como Newton-Raphson que aproxima las ecuaciones no lineales por su primer término de la serie de Taylor: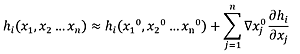
Con esta aproximación, el problema se convierte en lineal con el coste de necesitar iterar para conseguir converger a una solución próxima al óptimo. Sustituyendo h en la ecuación (1) se obtiene:
![]()
Agrupando los términos
![]()
se trata de resolver el sistema lineal G·x=b donde G es conocida como la matriz de ganancias.
Factorización QR
La resolución del sistema G·x=b nunca se realiza directamente invirtiendo la matriz G, donde típicamente se utiliza algún tipo de descomposición [1] que evita invertir la matriz.
Como se indica en [2], la matriz G suele presentar problemas numéricos de precisión y redondeo que pueden afectar a la convergencia del sistema o, en el mejor de los casos, a necesitar un mayor número de iteraciones para converger.
Por lo tanto, los autores recomiendan la factorización ortogonal QR que evita el cálculo directo de G y prácticamente eliminar los problemas numéricos asociados a la matriz de ganancias:
![]()
Sustituyendo en la ecuación (2), se obtiene:
![]()
Y considerando que Q ortogonal,
![]()
se obtiene la expresión final:
![]()
La ecuación (3) puede resolverse por sustitución directa ya que R es una matriz triangular superior. Esta ecuación es la base del estimador de estados que aquí se estudia y sobre la que se realizará la comparación con el nuevo algoritmo.
Limitaciones conocidas
La principal limitación de este enfoque es que no impone ninguna restricción a la capacidad de consumo o generación de los buses, lo que lleva a escenarios completamente irreales cuando se utiliza en cualquier red de distribución real. En [2] los autores proponen cómo modificar el planteamiento inicial para resolver un problema WLS con restricciones.
Otra limitación se encuentra en la dificultad de tratar elementos dinámicos como, por ejemplo, los reguladores de tensión en línea, cuyo comportamiento depende del valor del estado en cada iteración [2].
Por último, se ha de realizar una implementación eficiente del algoritmo cuando se trabaja con grandes redes (>100.000 buses), como programación multihilo para tratar bolsas independientes, uso de álgebra dispersa, etc.
Aun realizando la mejor implementación posible del algoritmo y aprovechando al máximo las capacidades actuales de las estaciones de trabajo, la dimensión del problema, es decir, el número de buses a manejar y por lo tanto el tamaño de la matriz de ganancias G representa el mayor desafío actual para su utilización en grandes redes en tiempo cuasi real.
Teniendo en cuenta que el tamaño de una variable de tipo ‘double’ es de 8 bytes y que la complejidad de la descomposición QR es 0(n3), y suponiendo el escenario favorable del tamaño mínimo posible de G, se muestra un ejemplo con una red de 1000 buses y otra de 2000 buses:

En el ejemplo de la tabla I, se muestra cómo doblando (x2) el tamaño de la red, se necesita x4 más de memoria y se aumenta la complejidad y por lo tanto los tiempos de cálculo en x8.
Si bien, el uso de la memoria puede aliviarse utilizando álgebra dispersa, la complejidad QR supone el principal obstáculo para una correcta utilización de estas técnicas en grandes redes de distribución que necesiten ejecutarse en tiempo cuasi real.
Fast Decoupled
La necesidad de mejorar la eficiencia de estos algoritmos ha llevado al desarrollo de la versión conocida como fast decoupled (FDSE) [3], basado en desacoplar la influencia de P y Q en las variables de estado y por lo tanto resolver dos matrices P-θ y Q-V y cada una con la mitad de filas y columnas que la matriz de ganancias original.
Tal y como se muestra en la Tabla I, aun teniendo que resolver dos sistemas, al tener la mitad de filas y columnas, presenta una gran mejora de eficiencia para sistemas grandes, donde no aporta casi diferencia para sistemas medianos o pequeños.
A pesar de las bondades de este enfoque en la mejora de velocidad y coste computacional, tiene dos importantes inconvenientes que deben tenerse en cuenta:
- En aquellos casos donde los parámetros de la red (como el ratio x/r) y las condiciones de operación violan las suposiciones realizadas para desacoplar las variables.
- Las medidas de corriente no comparten en general las suposiciones de desacople, por lo que este tipo de algoritmos no gestionan correctamente dichas medidas.
Estas limitaciones son lo suficientemente importantes para que impida utilizar la estrategia de desacople en muchas redes, donde tener que desechar todas las medidas de intensidad puede suponer una gran merma de información y por lo tanto un resultado menos preciso.
La motivación de este trabajo es presentar un algoritmo novedoso que consiga todos los beneficios de reducir la dimensión de la matriz de ganancias, pero sin los inconvenientes de los enfoques tradicionales como el fast decoupled. Para conseguir esto, se propone resolver el estimador de estados en el dominio de los números complejos en vez de realizarlo en el dominio de los números reales.
Algoritmo en el dominio complejo
Formular el algoritmo WLS en el dominio de complejo implica usar el conjugado de la variable compleja de tensión V* ϵ C en vez de usar la versión en forma polar |V| y θ ϵ R como variables de estado. Los principales beneficios de este enfoque son:
- Al igual que en la versión rectangular, las ecuaciones de potencia se expresan de forma exacta con un número finito de términos de la serie de Taylor y contiene sólo derivadas de orden 2 (fast exact second order state -FESOS-), en oposición a la versión en forma polar que requiere infinitos términos de la serie de Taylor.
- Las medidas de P y Q pueden expresarse en una única variable S=P+jQ , resultando en una reducción importante del número de filas, combinado con exactamente la mitad de variables de estado requeridas, se puede conseguir hasta una reducción de 4 veces el tamaño de la matriz de Ganancias y el Jacobiano obtenidos.
- Con el cambio de variable adecuado, se puede obtener un Jacobiano constante, que no dependa de las variables de estado, lo que implica otra gran mejora e impacto en los tiempos de cálculo.
Está demostrado que los sistemas FESOS proveen una solución precisa para todos los modos de operación, siendo muy superiores a otros algoritmos cuando se presentan sistemas mal condicionados. Pero incluso más importante, la reducción de hasta 4 veces el tamaño de la matriz de ganancias y un Jacobiano constante, implica una enorme ventaja cuando se trabaja con grandes redes.
Para ello, se utilizan las ecuaciones de potencia en su forma compleja y la matriz Jacobiana se construye con las derivadas parciales de la variable compleja V*, donde las medidas que se pueden utilizar son la inyección de potencia en un bus (Si) , el flujo de potencia entre dos buses (Sij) , la inyección individual de potencia en un bus (Pi, Qi ), el flujo de potencia individual entre dos buses (Pij, Qij), el módulo de la tensión en un bus (|Vi|) y el módulo de la corriente entre dos buses (|Iij|)
Cuando no se disponga de las medidas de P y Q simultáneamente, es posible utilizarlas de forma individual. Para ello, se utilizan las derivadas de Wirtinger para obtener las derivadas parciales de P y Q al formar el Jacobiano. De esta manera, no es necesario desechar las medidas de P y Q cuando se presentan de forma individual.
Formulación en el dominio complejo
Resolver el problema en el dominio complejo implica obtener el Jacobiano con las derivadas parciales de las ecuaciones de potencia con respecto al conjugado de la tensión que es la variable de estado elegida.
A continuación, se muestra el flujo de potencia en el modelo en de una línea de media distancia:
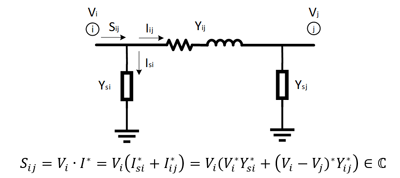
Dividiendo por , se obtiene el siguiente cambio de variable:
![]()
La ecuación (4) solo depende del conjugado de la tensión y, por lo tanto, sus derivadas parciales pueden obtenerse de forma directa:
![]()
Obsérvese que las derivadas parciales son constantes y no dependen de las variables de estado, lo que supone otra gran ventaja de esta formulación, puesto que no hay que recalcular el Jacobiano ni realizar la descomposición QR en cada iteración.
Para las medidas del módulo de la tensión y el módulo de la intensidad, se sigue la estrategia de suponer que las medidas son complejas (con módulo y ángulo), actualizando el ángulo con el valor obtenido en cada iteración. De esta forma se consigue que el cálculo de sus derivas parciales sea trivial y que mantenga constante el Jacobiano. Por el contrario, en cada iteración, hay que actualizar el valor de la medida con el valor del ángulo que se va obteniendo, operación que es mucho más eficiente que actualizar el Jacobiano en cada iteración.
Es decir, no solo se ha obtenido un Jacobiano mucho más sencillo (ver formulación en coordenadas polares [1][2][3]) y hasta 4 veces más pequeño, además se ha conseguido que sea constante, lo que supone otra gran mejora al tener que calcular G una sola vez.
Una vez obtenido el Jacobiano complejo, se procede a realizar la descomposición ortogonal para obtener la ecuación homóloga en (3), obteniendo la ecuación final en versión compleja:
![]()
Nótese que ahora sobre la matriz Q ha de realizarse la conjugada transpuesta, en vez de solo la transpuesta.
Resultados
La formulación clásica en variable real (ecuación 3), se va a comparar con la nueva formulación propuesta, en variable compleja (ecuación 5), en una red de distribución real, atendiendo no sólo a la precisión del resultado (error medio absoluto -MAE-) sino también a la eficiencia de recursos, principalmente memoria y tiempo de proceso.
Para ambas formulaciones se aplican todas las mejoras de eficiencia descritas por los autores en [2] como la simplificación de la matriz de admitancias, el uso de álgebra dispersa y la ejecución en paralelo de las bolsas detectadas.
La red elegida corresponde con una red real que cubre una gran área geográfica. A continuación, se muestran los resultados al ejecutar el estimador de estados desde su condición inicial, es decir, sin valor previo:

De los resultados obtenidos se desprende que ambas formulaciones obtienen prácticamente la misma precisión, siendo la diferencia del error medio absoluto despreciable. Donde sí se obtienen diferencias notables es en los recursos computacionales consumidos, con un incremento por parte de la formulación clásica de más del 73% en memoria y 90% en tiempo de cálculo.
Conclusiones
Se ha presentado un algoritmo novel, que resuelve el problema de la estimación de estados en el dominio de los números complejos, en vez de resolverlo en el dominio de los números reales. Este nuevo algoritmo presenta numerosas ventajas, como la de obtener mejores resultados con casos mal condicionados, una reducción de hasta 4 veces el tamaño de la matriz de ganancias y un Jacobiano constante.
Estas ventajas se traducen en una mejora sustancial en la eficiencia computacional, con ahorros en torno al 70% en memoria y del 90% en tiempo de cálculo para grandes redes de distribución de energía.
Estas virtudes presentan al nuevo algoritmo como el candidato ideal para las redes Smart Grid donde cada vez con más frecuencia, los centros de control demandan poder procesar y mostrar los resultados de forma precisa y en tiempo cuasi real.
Referencias
- Ali Abur & A. Gomez-Exposito, 2004, “Power System State Estimation Theory and Implementation”, CRC Press.
- Besada, et. al, 2019, “State estimation for large power distribution systems”, ICREPQ’19.
- John J. Grainger & William D. Stevenson, 1994, “Power System Analysis”, McGraw-Hill.
- Dehghanpour, et al, 2018, “A Survey on State Estimation Techniques and Challenges in Smart Distribution Systems”, IEEE.
- Tomasz Okon & Kazimierz Wilkosz, 2010, “Comparison of Weighted-Least-Squares Power System State Estimation in Polar and Rectangular Coordinate Systems”, IEEE.
- Yousu Chen, 2015, “Weighted-Least-Square State Estimation”, PNNL.