Comunicación presentada al V Congreso de Smart Grids
Autores
- Leonidas Sayas, Gerente de Supervisión de Electricidad, OSINERGMIN
- Ruben Felix, Especialista, RELP2010 SAC
Resumen
La presente comunicación evalúa el problema de las inflexibilidades que existen en los sistemas eléctricos de potencia que tienen un alto grado de penetración de energías renovables intermitentes debido a la presencia de equipos convencionales. Se toma como estudio de caso un sistema real existente en la parte sur del Perú para el cual se generan series temporales sintéticas que permiten simular la producción de futuras plantas solares y eólicas a construi. Éstas son posteriormente analizadas dentro de un modelo matemático de optimización que realiza un despacho económico, incluyendo dentro de su formulación el compromiso de unidad, la generación hidráulica, el flujo de potencia a través de línea de transmisión y la generación forzada de centrales renovables no gestionables. Finalmente, se realiza una comparación de los resultados obtenidos entre un escenario base y dos escenarios alternativos que introducen el concepto de “Smart Generation”, el cual consiste combinar centrales intermitentes con grupos términos ultra flexibles.
Palabras clave
Energías Renovables, Generación Distribuida, Inflexibilidades, Optimización, Smart Generation
Introducción
Las importantes reducciones en costos que las tecnologías de generación a base energías renovables no convencionales (ERNC) han registrado de manera sostenida en los últimos años (International Energy Agency, 2016), han permitido que las inversiones en nuevas plantas ERNC realizadas en países en vías de desarrollo superen a los montos desembolsados por los países que adoptaron estas tecnologías en sus inicios. En muchos casos, estas tecnologías representan una gran oportunidad para cerrar las brechas de electrificación de las zonas rurales de estos países, o una alternativa de solución a los problemas de calidad del servicio eléctrico de zonas abastecidas por sistemas baja confiabilidad (Sayas et al, 2017).
En consecuencia, la presencia de las ERNC en los sistemas eléctricos se ha visto incrementada. Este aumento dentro de las matrices de producción de energía eléctrica, ha puesto de manifiesto los problemas de inflexibilidad que los sistemas convencionales ocasionan. Así, la cuantificación de las inflexibilidades ha sido abordada en diversas publicaciones como (Lannoye et al, 2012) que propone el empleo de determinadas métricas a fin de incluir dentro de los estudios de planeamiento y operación esta problemática. Los problemas de inflexibilidad redundan en sobrecostos operativos que distorsionan el funcionamiento eficiente de los mercados eléctricos, como lo ocurrido en Alemania donde se llegaron a tener tarifas eléctricas negativas.
Recientemente en (Sayas et al, 2017), se presentó un modelo estocástico de optimización que permite elegir el mix óptimo de centrales de generación distribuida renovable que ayudan a mejorar la confiabilidad de sistemas eléctricos críticos que, sin embargo, no logra evaluar completamente el impacto que tendría la intermitencia de las ERNC en la operación del sistema. Evidentemente, tal como lo menciona (Alsaidan et al, 2016), la presencia de fuentes intermitentes exige la integración de sistemas capaces de respaldarlos y ofrecer una potencia firme hacia la red.
Los actores que vienen ganando mayor impulso para hacer frente a estos requerimientos son los sistemas de almacenamiento, los cuales pueden soportar numerosos tipos de aplicaciones y requerimientos (Winfield et al, 2018). Sin embargo, sus elevados costos actuales y poco tiempo de vida útil hacen que su implantación no sea óptima. No obstante, el desarrollo y mejora de las tecnologías convencionales ofrecen también nuevas alternativas de generación que superan las limitaciones tradicionales. Así, como se demuestra en (Rautkivi et al, 2013), el empleo de máquinas térmicas ultra flexibles resuelve los problemas causados por la intermitencia de recursos renovables y las inflexibilidades de las unidades de generación convencionales, logrando una transición entre ambas tecnologías.
En esta comunicación se presenta un análisis de los efectos de la generación renovable intermitente dentro de un pequeño sistema eléctrico real con alto grado de penetración de ERNC y las mejoras obtenidas por la inclusión de equipos ultra flexibles.
Metodología
Efecto de las inflexibilidades
La flexibilidad de un sistema eléctrico representa la capacidad que tiene de empelar sus recursos para responder a los cambios en la demanda neta, que es aquella demanda que no es suministrada por las fuentes de generación variable (Lannoye et al, 2012). Las inflexibilidades tienen su origen en parámetros como 1) rampas máximas de subida o bajada de generación, 2) tiempos mínimos de operación o entre arranques, 3) potencias máximas de arranque y parada; etc.
Aunque (Lannoye et al, 2012) propone el empleo de métricas especializadas y complejas para determinar el grado de flexibilidad (o inflexibilidad) de un sistema, una forma práctica de cuantificarla es haciendo uso de los parámetros Energía No Suministrada (ENS) y Excedente de Energía Generada (EEG). Estos parámetros, para sistemas sin problemas de capacidad de generación o transmisión, refleja el efecto de las inflexibilidades que no permiten satisfacer, por ejemplo: las rampas de subida o bajada que exige la demanda.
Centrales renovables no convencionales intermitentes
Esta comunicación parte del sistema obtenido en (Sayas et al, 2017), que muestra un plan de expansión a 10 años. Consecuentemente, en esta comunicación se emplean técnicas estadísticas para la síntesis de series temporales que permitan simular el comportamiento intermitente de las centrales solares y eólicas a construir en el futuro.
Centrales eólicas
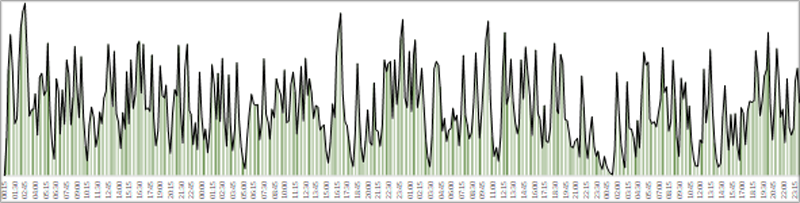
Partiendo de los parámetros de la distribución Weibull que caracterizan a la distribución de frecuencias de la velocidad del viento, se generan valores aleatorios para intervalos de 15min. Estos valores son convertidos en potencia utilizando las curvas de potencia de un aergenerador referencial.
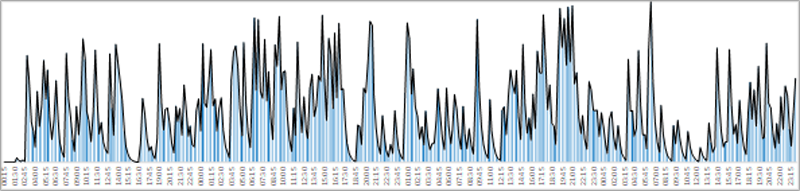
En este proceso, se debe tener especial cuidado en no generar series muy correlacionadas entre sí, ya que esto afectaría la representación del comportamiento estocástico del recurso dentro del modelo matemático.
Centrales solares
Para el caso de las centrales solares se emplea una distribución normal trunca entre los valores mínimos, promedio y máximo de irradiación solar obtenida para un día típico de cada mes. Estos valores generados de manera aletoria son luego desagregados para intervalos de 15 min haciendo uso de las ecuaciones de geometría solar y relacionadas (Duffie et al, 2013). Finalmente, tomando en consideración el efecto de la tempertura y las características técnicas un panel fotovoltaico referencial, se obtiene una serie de tiempo para la producción solar.
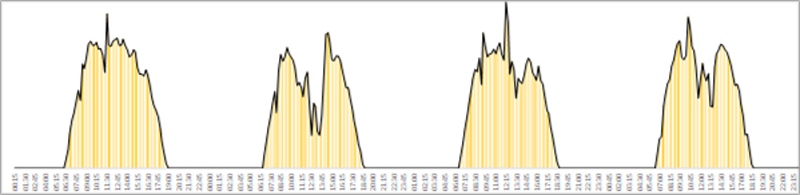
Se introduce ruido dentro de la serie temporal a fin de reflejar las variaciones en la producción que existen por las sobras, nubes y demás factores que afectar a estos sistemas.
Modelo matemático de optimización
El modelo matemático propuesto toma parte de la formulación presentada en (Morales-España et al, 2013) que desarrolla restricciones compactas para el problema de compromiso de unidad, y lo combina con lo planteado por (Sayas et al, 2017) que presenta un modelo de planificación a largo plazo con generación distribuida RER.
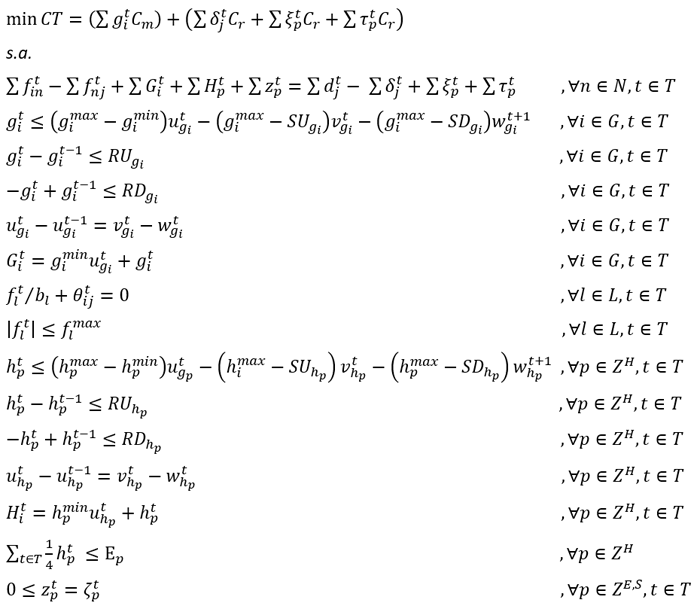

El modelo emplea las restricciones de (Morales-España et al, 2013) para representar las limitaciones de rampa de subida y bajada de potencia de las centrales convencionales, así como para indicar las máximas potencias que pueden tomar en el arranque o parada. El estado operativo de la unidad se representa por variables binarias que se relacionan lógicamente con las variables y que indican cuando un grupo se enciende o se apaga respectivamente. En esta comunicación no se consideran los tiempos mínimos de operación o entre arranques, o los costos de arranque y parada de las unidades térmicas por limitaciones computacionales.
Dentro del modelo también se consideran variables de holgura que ayudan a la convergencia del modelo, pero al mismo tiempo capturan los valores de demanda no atendida ( ), energía renovable no aprovechada o desperdiciada ( ) y generación convencional de excedente debido a inflexibilidades de su operación ( ).
Estudio de caso
El modelo matemático es aplicado sobre un sistema real existente en el sur de Perú que fue presentado inicialmente en (Sayas et al, 2017). Se emplean intervalos de 15 minutos como paso de simulación pues permiten capturar mejor el comportamiento estocástico de las cargas eléctricas y las centrales de generación ERNC. Por otro lado, la capacidad de las plantas solares y eólicas han sido incrementadas hasta lograr un grado de penetración de aproximadamente 65% de la generación total a fin de obtener mayor claridad en el análisis y las comparaciones. La implementación del modelo se realiza en lenguaje AMPL y se hace uso del solver Gurobi ofrecido por la plataforma en la nube NEOS Server.
Descripción del sistema
El sistema eléctrico ubicado en Puno, Perú (Sistema EPU) está conformado por 25 nodos, 25 líneas de transmisión, 10 puntos de demanda y 12 centrales de generación (entre solares, eólicas e hidroeléctricas) como se ve en la Fig. 4. Se analizada un horizonte 576 pasos equivalentes a 6 días o 144 horas o 8640 minutos. Cada día representa un día típico de los meses de enero a junio (Duffie et al, 2013).
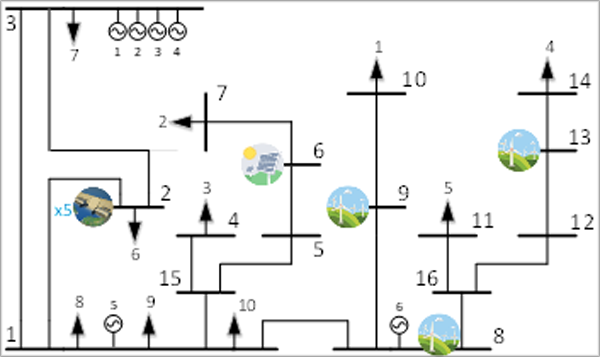
Resultados obtenidos
Se analizan tres escenarios. El primer escenario muestra el comportamiento normal del sistema que tiene un grado de penetración de generación intermitente de 65%. El segundo escenario introduce un grupo término a gas ultra flexible en la barra 3. Finalmente, el tercer escenario muestra la performance del sistema cuando se implementan dos grupos adicionales en las barras 1 y 8. En definitiva, se simula el comportamiento del Sistema EPU cuando se implementa el concepto de “Smart Generation” que combina centrales intermitentes con grupos ultra flexibles.
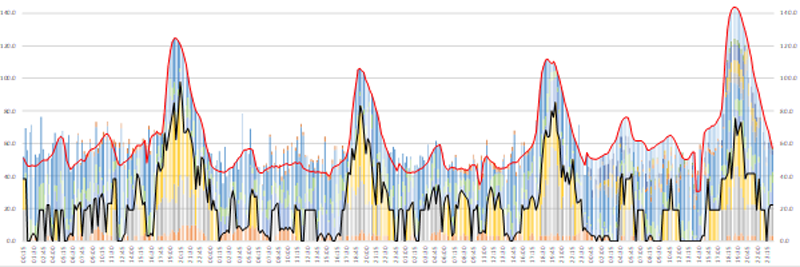
Primer Escenario: Sin Smart Generation
Para el primer escenario, las inflexibilidades de los grupos convencionales ocasionan que se generen 4.1% más energía de la que es requerida por la demanda. Sin embargo, la demanda no es satisfecha en todo momento, llegándose a un total de 27.2 MWh de energía no suministrada.
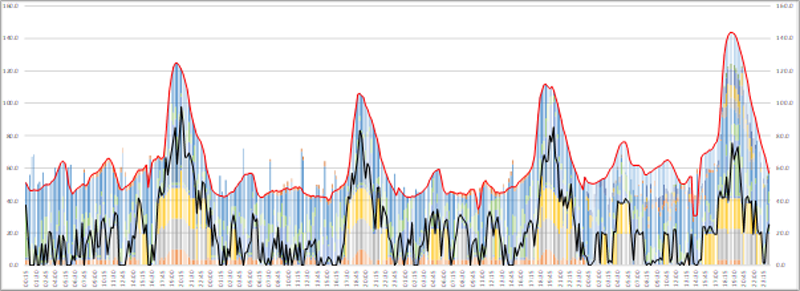
Segundo Escenario: Con Smart Generation – Una unidad ultra flexible
Para el segundo escenario, las inflexibilidades y la intermitencia son contrarrestadas con la operación de una unidad ultra flexible. Así, la generación ahora excede tan solo en 2% a la demanda. En este escenario todavía existe demanda no satisfecha pero solo representa un total de 0.2 MWh de energía no suministrada.
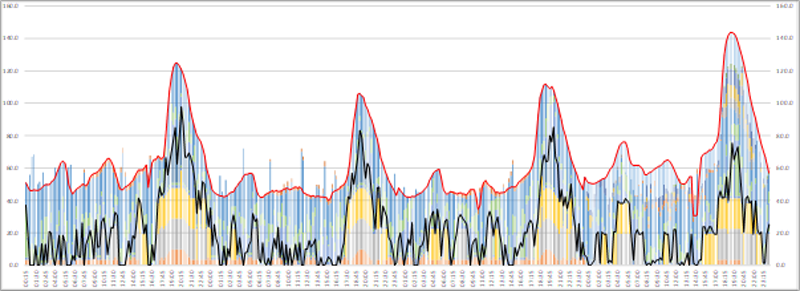
Tercer Escenario: Con Smart Generation – Tres unidades ultra flexibles
En el tercer escenario, a pesar de la inclusión de dos unidades ultra flexibles adicionales, la generación excedente se mantiene en 2% y la energía no suministrada en 0.2 MWh.
Conclusiones
El modelo deasarrollado permite analizar el comportamiento de los sistemas eléctricos con presencia de centrales de ERNC intermitentes. Asimismo, logra evaluar el impacto ocasionadas por las inflexibilidades operativas de los grupos convencionales.
Las simulaciones realizadas muestran que, ante un alto grado de penetración de ERNC la demanda queda insatisfecha o se producen excedentes de generación eléctrica en varios momentos (desbalances energéticos). Asimismo, se evidencia que la inclusión de un único grupo ultra flexible reduce en 50% y 99% la EEG y la ENS, respectivamente. Mediante la corrección de estos desbalances se mejoran los perfiles de tensión, se reducen las pérdidas de potencia activa y se logran postergar inversiones que, de otra forma, deberían realizarse.
Finalmente, se nota que, la inclusión de unidades ultra flexibles adicionales en este sistema no aporta mayor beneficio operativo. En consecuencia, se recomienda 1) realizar estudios sobre el nivel óptimo de penetración ERNC, 2) aumentar la demanda mediante interconexiones con otros sistemas, o 3) evaluar la conveniencia de incluir sistemas de almacenamiento de energía para capturar la energía sobrante y re-inyectarla en los momentos de déficit.
Referencias
- Alsaidan, I. et al (2016), “Determination of Battery Energy Storage Technology and Size for Standalone Microgrids,” Power and Energy Society General Meeting (PESGM), Estados Unidos.
- Duffie, J. & Beckman, W. (2013), “Solar Engineering of Thermal Processes,” 4ta Edición, Wiley, Estados Unidos.
- International Energy Agency (2016), “World Energy Outlook 2016” [En línea].
- Lannoye, E. et al (2012), “Evaluation of Power System Flexibility,”. IEEE Transactions on Power Systems, 27(2), 922–931.
- Morales-España, M. et al (2013), “Tight and Compact MILP Formulation for the Thermal Unit Commitment Problem,”. IEEE Transactions on Power Systems, 28(4), 4897–4908.
- Rautkivi, M. et al (2013), “Future Market Design for Reliable Electricity System in Europe,” POWERGEN Europe 2013, Austria.
- Sayas, L. & Felix, R. (2017), “Modelo Estocástico Multietapa para la Selección del Mix Óptimo de Generación Distribuida Renovable en Sistemas Eléctricos Críticos,” IV Congreso Smart Grids, España.
- Winfield, M. et al (2018). “Energy policy regime change and advanced energy storage: A comparative analysis,”. Energy Policy, 115, 572–583.