Comunicación presentada al IV Congreso Smart Grids:
Autores
- José Herrera García, Ingeniero RAMS y LCC, Patentes Talgo
- Abderrahim Khamlichi, Ingeniero, Centro Tecnológico de Alta Tensión (LCOE)
- Fernando Garnacho, Director, Departamento de Alta Tensión (LCOE)
Resumen
Debido al incremento de la demanda de potencia en las ciudades, líneas eléctricas subterráneas han sido añadidas gradualmente en las ya utilizadas galerías, que representan una nueva solución que permite un mantenimiento sencillo y aislado. Una línea eléctrica de transporte de alta tensión genera un gran campo electromagnético a su alrededor, afectando así a las líneas eléctricas cercanas. La estimación de estado es crucial para la gestión online en las nuevas Smart Grids, sin embargo, en algunos casos su uso no es correcto por el desconocimiento de las impedancias de la red. En este artículo se realiza un estudio sobre la influencia que genera la proximidad de una línea eléctrica de transporte en las impedancias de una red eléctrica de distribución que circula cercana a ella por la misma galería, y las consecuencias en la estimación de estado.
Introducción
La estimación de estado juega un papel fundamental en los sistemas SCADA con el objetivo de observar y controlar eléctricamente los sistemas de potencia, y se ha puesto mucho esfuerzo en el desarrollo de diferentes métodos para las líneas de transporte, y en los últimos años en las redes de distribución.
Particularmente se ha puesto mucho hincapié para afrontar la falta de medidas redundantes en las redes de distribución. Una propuesta es el uso del llamado “Forecasting Aided State Estimation” (FASE) [1]. De la misma manera, en el proyecto europeo [2], un método para observar el sistema llamado “Nodal Load Observer” (NLO) fue desarrollado. De forma parecida a la mayoría de los métodos FASE, el método NLO usa un simple modelo de cargas para predecir la evolución en el tiempo del estado del sistema.
La calidad del estimador de estado resulta crucial en la gestión online de los sistemas de potencia y numerosos estudios se han publicado para dar una perspectiva general de la estimación de estado y el control para Smart Grids [3]. Sin embargo, en esos estudios la incertidumbre asociada a la medida es normalmente una estimación ad-hoc, y esta incertidumbre tiene una falta de perspectiva metrológica cuando en la realidad las incertidumbres deben ser consideradas en los algoritmos.
En el proyecto [2] se determinan las contribuciones de la incertidumbre a la estimación de estado del flujo de potencia y se desarrolla un método para encontrar el emplazamiento óptimo del sensor con el objetivo de conseguir la incertidumbre más baja. Sin embargo, esta propuesta no tiene en consideración la incertidumbre de la topología de la red como por ejemplo la incertidumbre de la impedancia de la línea. En su lugar, estos parámetros eran asumidos como conocidos, lo que no se asemeja a la realidad. Un proyecto reciente [4] que comenzó hace 3 años, desarrolla una propuesta para emplear métodos de estimación de estado para estimar las impedancias de las líneas eléctricas. Este intenta incrementar la veracidad de los estimadores de estado, pero la influencia que genera el acoplamiento magnético en las líneas de alta tensión [5] es analizada en esta comunicación.
Descripción de la red diseñada
El análisis de este estudio ha sido desarrollado en una red de distribución secundaria de 20 kV, que consiste en 19 diferentes subestaciones MT/BT denominadas como nudos. Esta red de media tensión suministra energía a un área de la ciudad de Málaga, donde cada uno de los nudos demanda una potencia específica. Las 19 subestaciones MT/BT están interconectadas mediante 18 tramos de línea, 14 de ellos están instalados mediante zanja, y los otros 4 tramos transcurren a lo largo de una galería. La conexión de las pantallas a tierra es mediante solid-bonding para cada sección de la red de distribución.
Una línea de transporte de 220 kV está localizada en la misma galería que la red de distribución de 20 kV. Ambas redes transcurren a lo largo de la misma galería durante los 4 tramos anteriormente mencionadas, lo que supone 1.5 km de un total de 5.7 km (ver figura 1). Cuando la línea de transporte está cargada, esta genera un campo electromagnético que afecta a las impedancias de la red de distribución, y consecuentemente a los resultados de la estimación de estado.
Esta influencia generada depende de la configuración de los cables (tresbolillo o en capa) y la distancia entre ambas redes eléctricas.
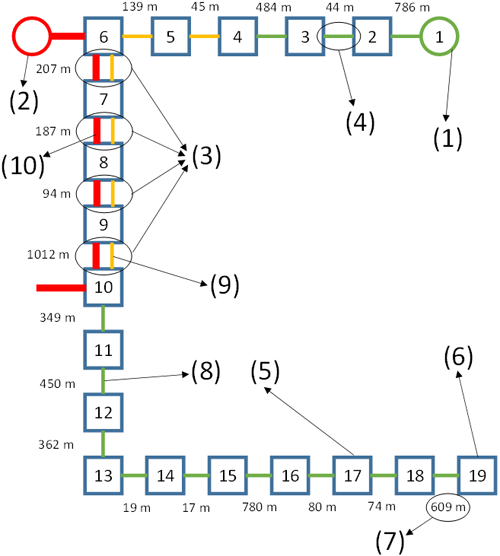
Todos los tramos en zanja y en galería de la red de distribución de 20 kV presentan una configuración de cables al tresbolillo, sin embargo, la configuración de los cables de la línea de transporte va a presentar diferentes configuraciones, de cara a poder observar el comportamiento del estimador de estado.
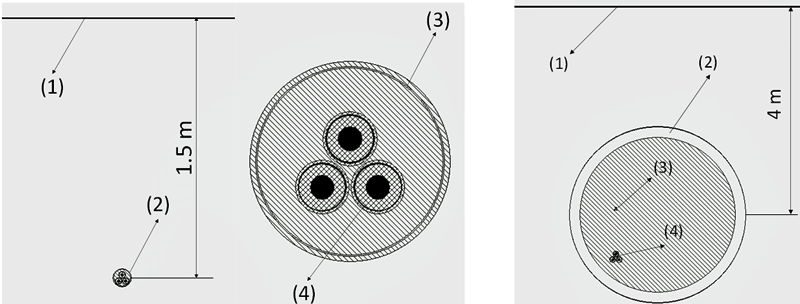
La zanja diseñada para la red de distribución tiene una distancia de enterramiento de 1.5 m, y los cables están en contacto en el interior de una tubería de 0.15 m de diámetro (ver fig. 2), mientras que la galería diseñada para la red tiene una distancia de enterramiento de 4 m, y consiste en un túnel de hormigón de 3 m de diámetro (ver fig. 3).
La distribución del suministro de potencia en la red de distribución de 20 kV se presenta en la tabla I. De acuerdo con la tabla I, el nudo 3 es el único nudo que aporta potencia a la red, los demás nudos son consumidores de potencia.
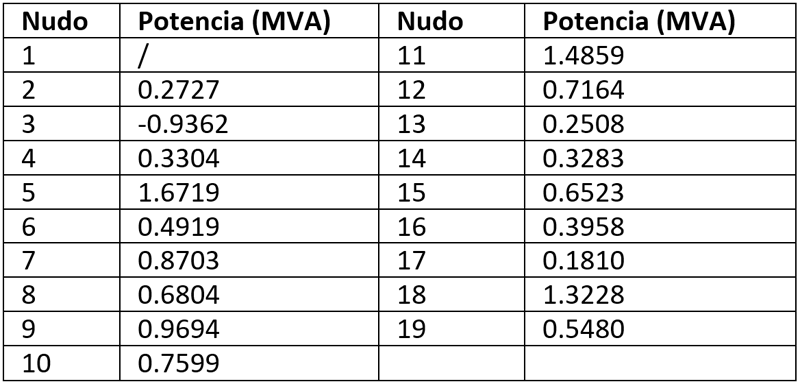
Es estudio ha sido realizado para el régimen estacionario, en el cual la red de distribución suministra 11 MVA, y la línea de transporte suministra 400 MVA. Se ha considerado para los cálculos un factor de potencia de +0.8 para ambas redes. Los resultados se van a exponer en sistema por unidad, considerando 1 MVA y 20 kV como las bases de potencia y de tensión respectivamente, así pues, la impedancia base resulta 400 Ω.
Estimador de estado diseñado para la red de distribución
Se ha diseñado un algoritmo para la estimación de estado de la red de distribución, con el objetivo de poder observar la influencia que causa la inclusión de la línea de transporte en la galería. La estimación de estado está basada en el método de mínimos cuadrados ponderados, y está implementada en Matlab con el algoritmo de Levenberg-Marquardt.
La ecuación para la estimación de estado es la que sigue a continuación:
(1)
donde: (siendo m ≥ n).
Zm es el vector de medidas (m x 1)
x es el vector de variables de estado que ha de ser estimado (n x 1);
h es un vector de funciones no lineales que relaciona las variables de estado con las
F es el vector de errores (m x 1)
En este estudio, el vector de medidas Zm está compuesto de las potencias inyectadas en los nudos y las potencias de flujo, y el vector x de variables de estado está formado por las tensiones de los nudos que no presentan medida.
Validación del estimador de estado
El mejor modelo de estimador de estado que se ha conseguido ha sido aquel que tiene medidas en los nudos 1, 3, 6, 9, 12, 15, 18 (ver fig. 3).
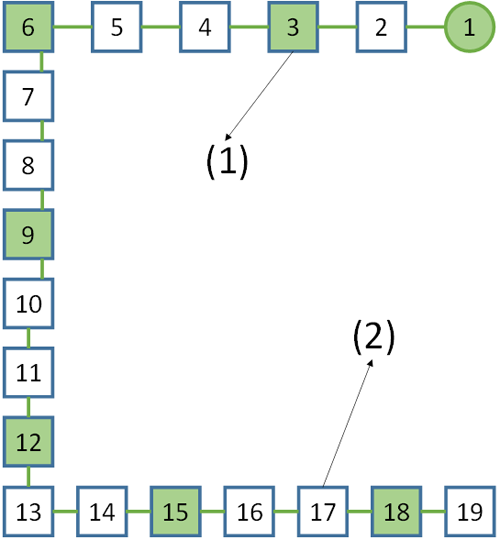
Los resultados obtenidos con el estimador de estado permiten afirmar que este funciona correctamente, ya que las diferencias entre los resultados del estimador y los valores reales presentadas en la Tabla II son insignificantes y aceptables para un estimador.
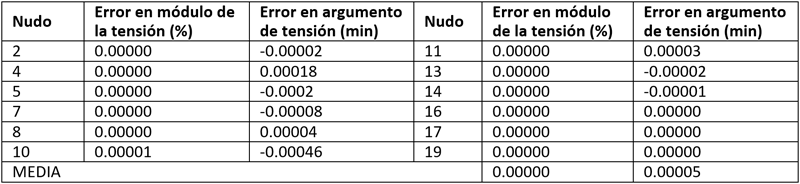
Influencia de la línea de transporte en la medida de la red de distribución
En este apartado se estudian las diferencias que introducen en las medidas y por tanto en el estimador de estado la línea de transporte al 100% de carga con diferentes disposiciones (casos estudiados dependiendo de la configuración que tiene la galería).

Se ha comprobado que las diferencias introducidas en el módulo de la tensión son inexistentes. Para el argumento de la tensión las diferencias son también muy pequeñas, sin embargo, la diferencia porcentual es muy significativa, siendo 15-25% valores comunes para los diferentes casos estudiados. Las variaciones introducidas en los argumentos son el principal problema para el estimador de estado. Estas están relacionadas con la distancia existente entre ambas redes eléctricas y las distintas formaciones de los cables. En las siguientes figuras aparecen ilustrados algunos de los resultados más significativos obtenidos a lo largo de este estudio, que demuestran lo anteriormente comentado.
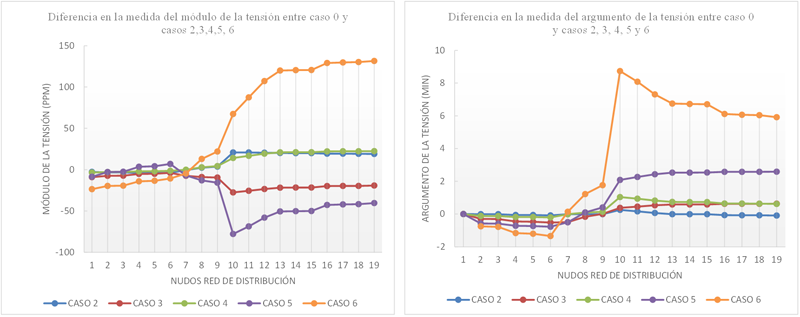
Como se puede observar en la figura 5, el desequilibrio en la medida se produce en torno a los nudos 6, 7, 8, 9 y 10, que son los nudos pertenecientes a la galería, por lo que se puede afirmar que la línea de alta tensión afecta a las medidas directamente. Además, la mayor diferencia se produce en el nudo 10, que coincide con el tramo más largo de la galería. La configuración en capa produce una mayor variación en las medidas que la configuración en tresbolillo (ver caso 2 comparado con caso 3, y caso 4 comparado con caso 5). La razón por la que sucede es que en un sistema trifásico al tresbolillo, los campos magnéticos generados por las corrientes que circulan en los cables se cancelan unos a otros.
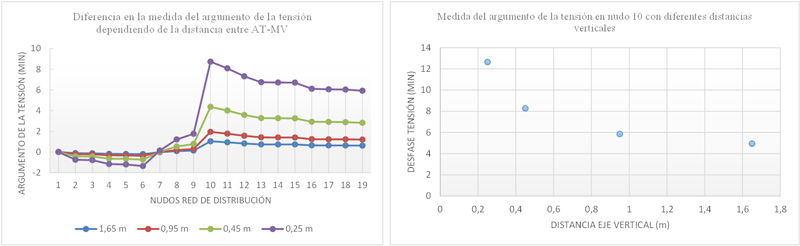
La figura 6 demuestra que la distancia existente entre la línea de transporte y la red de distribución tiene una influencia exponencial en el argumento de la tensión. En la parte derecha de la imagen, se puede observar la medida del argumento de la tensión para el nudo 10, donde se observa de forma más clara esta influencia exponencial.
Influencia de la línea de transporte en el estimador de estado
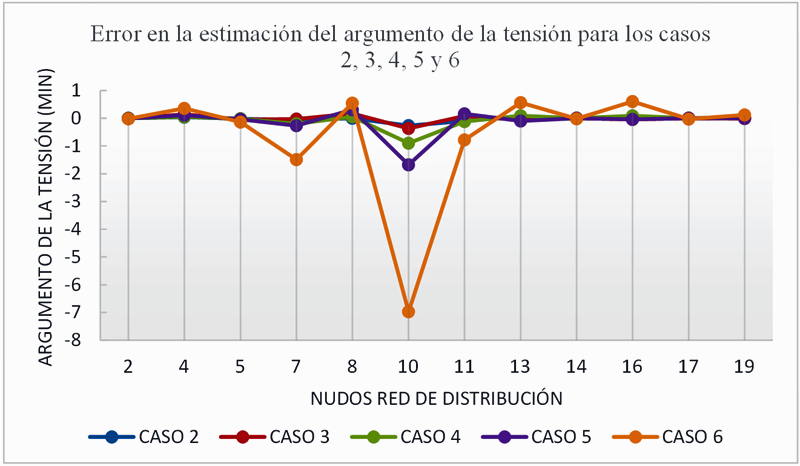
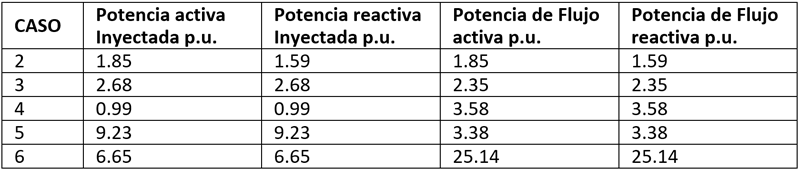
La figura 7 muestra el error que existe en el argumento de la tensión que es calculado por el estimador de estado para los diferentes casos estudiados (los nudos con medida no están incluidos puesto que el error es 0). Como se puede observar, los resultados que proporciona el estimador de estado no son correctos, e introducen errores en las medidas. Se ha comentado en el anterior apartado que los errores son pequeños, pero que la diferencia porcentual que producen es muy significativa. Para demostrar lo anterior de manera objetiva se pone como ejemplo la tabla III, donde se representan los errores máximos de las potencias calculadas por el estimador de estado para los diferentes casos. Estos errores se introducen debido a las diferencias porcentuales de los argumentos de la tensión. Como se puede observar son errores muy abultados, y no admisibles en un sistema de gestión de energía como podría ser la gestión online de una Smart Grid.
Conclusiones
Los sistemas de protección de la red de distribución no van a ver afectado su funcionamiento debido a la inclusión de la línea de transporte en la galería. El principal problema es la gestión de la potencia en la red de distribución, pues los módulos y en menor medida los argumentos de las tensiones están estimados dentro de unos valores aceptables. Si se deseara continuar controlando la gestión de la red de distribución con el estimador de estado, este debe ser modificado. La solución óptima para el control de la red es el diseño de un estimador de estado que dependiendo de la carga que circule por la línea de transporte, modifique la matriz de admitancias nodales de su base datos.
Agradecimientos
El estudio reflejado en el artículo ha recibido apoyo desde el programa EMRP, que ha sido fundado por los países participantes en EURAMET y la Unión Europea (ENG63).
Referencias
Yih-Fang Huang; Stefan Werner; Jing Huang; Neelabh Kashyap; Vijay Gupta. “State estimation in electric power grids Meeting new challenges presented by the requirements of the future grid”, Browse Journals & Magazines; IEEE Signal Processing Magazine; Vol. 29 Issue: 5; 22nd August 2012; DOI: 10.1109 /MSP.2012.2187037
”Metrology for Smart Electrical Grid”; EURAMET- JRP ENG04 SmartGrids, http://www.smartgrid-metrology.eu/
Md Masud Rana and Li Li. “An Overview of Distributed Microgrid State Estimation and Control for Smart Grids”; Sensors 2015, 15, 4302-4325; doi:10.3390/s150204302
ENG63 “Sensor network metrology for determination of electrical grid characteristics” European Metrological Research Program, 2014.
J. Herrera, J. Martínez, A. Khamlichi “Influencia de la proximidad de líneas subterráneas de transporte en la estimación de estado de redes de distribución secundaria”, ETSII, Madrid, 2017.