Comunicación presentada al IV Congreso Smart Grids:
Autores
- Leónidas Sayas, Gerente de Supervisión de Electricidad, OSINERGMIN
- Rubén Félix, Especialista, RELP2010 SAC
Resumen
La presente comunicación desarrolla un modelo matemático de optimización dinámica que permite obtener el mix óptimo de centrales de generación con recursos energéticos renovables (RER) necesarios para dotar de confiabilidad a sistemas eléctrico críticos, soportando de esta forma uno de los pilares de las Smart Grids: la continuidad del suministro y la reducción de los tiempos de interrupción. Este modelo toma como entrada el potencial energético de recursos hídricos, eólicos y solares disponibles e inyectables en la zona, los costos de inversión de estas centrales y de su infraestructura eléctrica relacionada; así como las características de la red de transmisión y centrales convencionales existentes. La simulación es realizada para las 8760 horas de un año típico dentro del cual se considera estados de falla (fuera de servicio) para las líneas de transmisión, barras y centrales existentes. Dentro de su enfoque estocástico se contempla un análisis de sensibilidad de los costos. Los resultados en un caso de aplicación real muestran mejoras de aproximadamente 90% en los índices SAIFI y SAIDI de calidad del servicio eléctrico en el sistema.
Introducción
La evolución de los sistemas eléctricos existentes hacia el concepto de las Smart Grids pasa por muchos factores importantes. Uno de estos es la mejora de la continuidad del servicio y la reducción de los tiempos de interrupciones. Para cumplir este objetivo, además de implementar sistemas de comunicación y equipos inteligentes que permitan reconfigurar las redes para minimizar las zonas de impacto de las fallas o aplicar técnicas de Big Data para predecir la demanda y preparar el sistema para atenderla, también se debe dotar de resiliencia por el lado de la oferta haciendo uso del concepto de generación distribuida. Recientemente las tecnologías de generación a base de recursos energéticos renovables (RER) han registrado importantes reducciones en sus costos de inversión, con una clara tendencia a seguir reduciéndose en los próximos años al mismo tiempo que sus eficiencias van en aumento (International Energy Agency, 2016) por lo que se han convertido en una buena alternativa de solución para lograr acercar la generación a los centros de consumo evitando altos costos en infraestructura de transmisión, pérdidas técnicas y mejorando los perfiles de tensión de las zonas en donde son instaladas.
Muchos trabajos han abordado el problema de la planificación y operación de los sistemas eléctricos considerando la penetración de estas nuevas tecnologías intermitentes. Así en (Tang et al, 2015) se aborda el problema de la planificación de la expansión de la transmisión (TEP) considerando la penetración de plantas eólicas desde un punto de vista estocástico, mientras en (Zheng et al, 2015) se busca optimizar las inversiones en transmisión haciendo uso de baterías para “cortar los picos y rellenar los valles” de la generación renovable intermitente. Otros trabajos como (Barbosa et al, 2016) combinan TEP con la planificación de la expansión de la generación (GEP) e incorpora un análisis de sensibilidad de los costos para obtener soluciones robustas ante incertidumbres.
En esta comunicación se presenta un modelo matemático de optimización dinámica estocástica capaz de realizar un proceso de optimización considerando las 8760 horas de un año típico a fin de decidir el mix óptimo de centrales de generación distribuida renovable que deben ser construidas para dotar de confiabilidad y mejorar la calidad de los sistemas eléctricos críticos, que son aquellos en donde se presenta una alta tasa de interrupción del suministro eléctrico y largos períodos de tiempo para su restablecimiento.
Metodología
Evaluación de la calidad de un sistema eléctrico
Para la medición de la calidad de un sistema eléctrico se hace uso de los indicadores SAIFI y SAIDI.

Estos dos índices se calculan generalmente para periodos anuales y permiten hacer un seguimiento de la evolución de la calidad de los sistemas eléctricos. Mientras más altos sean estos valores, más crítico será considerado un sistema. En esta comunicación se utilizan ambos índices para comparar los resultados obtenidos.
Modelamiento de las restricciones
Además de las restricciones para el despacho de las centrales de generación convencional gti , el flujo de potencia ftl y el planeamiento de la transmisión wl; se hacen uso de restricciones novedosas para la simulación de proyectos de energías renovables.
Centrales de generación renovable
A diferencia de las centrales hidroeléctricas htp, se debe tener presente que la generación no convencional, solar y eólica, es intermitente, tal como se muestra en la Fig. 1. Para estas tecnologías no existe mayor control sobre su despacho, así todo lo que se genera en cada instante ztp debe ser despachado al sistema ztp.
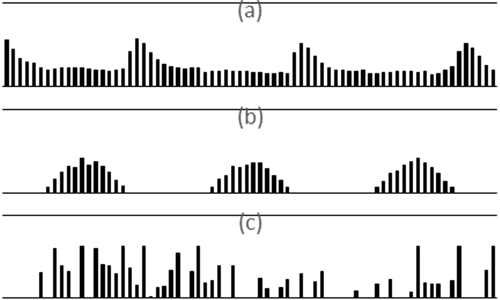
Cada posible central tiene asociada una o más líneas de transmisión con distintas capacidades de potencia, que van en el rango de -25% a +25% la potencia nominal instalada de la central, que pueden servir para interconectar la planta al sistema. Estas alternativas buscan evitar la implantación de líneas que luego queden con factores de uso demasiado bajos o que impongan limitaciones al despacho (Zheng et al, 2015). La producción hidráulica, por su parte, se ve limitada a una cantidad anual de energía Ep que la central es capaz de suministrar dependiendo de sus condiciones geográficas, hidrológicas y constructivas.
Para aquellos lugares donde una misma área de terreno puede servir para implantar o una planta solar o una eólica ZArea, se debe evitar la superposición de estos proyectos. Debe realizarse también un análisis particular para cada barra a fin de determinar cuánto es la máxima potencia intermitente que se puede inyectar Bmaxj. Esta limitación no incluye a las centrales hidroeléctricas ya que estas máquinas si aportan inercia y mas bien contribuyen a reforzar la estabilidad del sistema.
Balance nodal de potencias
Debido a que no siempre es posible lograr un balance perfecto entre oferta y demanda, es necesario incluir dos variables importantes al modelo. La variable stj que representa a la demanda no atendida o racionada y que indica la potencia renovable desperdiciada o que no puede ser consumida.
Función objetivo
La función de costo total CT está conformada por tres componentes. Primero, el costo de generación CG que valoriza al costo marginal de mercado Cm la producción de las centrales convencionales. Luego, el costo de racionamiento y desperdicio CR que utiliza un valor muy alto Cr para penalizar la demanda no atendida y la generación renovable no aprovechada. Y por último, el costo de proyectos CP que considera la anualidad del costo de inversión y el costo anual de operación y mantenimiento de las líneas de transmisión y centrales RER que se hayan decidido construir. Dado que Cm < Cr, esta función objetivo logra maximizar la penetración de energías renovables al penalizar el desperdicio de su generación (Ugranli & Karatepe, 2013). El modelo matemático completo se muestra en (3).
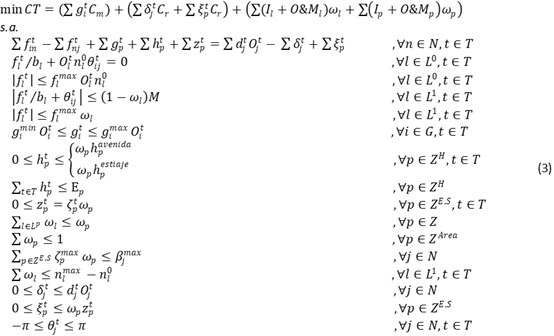
Optimización estocástica
Mediante la incorporación de la expresión (4) se añade una aproximación estocástica al modelo. Esta ecuación realiza un análisis de sensibilidad de costos dentro del proceso de optimización que le permite al modelo decidir la mejor combinación de centrales renovables considerando incertidumbres en sus costos.
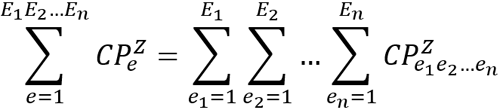
Caso de estudio
El modelo matemático desarrollado es aplicado sobre un sistema real existente en el Perú. La implementación del modelo se realiza en el lenguaje AMPL y se hace uso del solver Gurobi ofrecido por la plataforma de computación en la nube NEOS Server.
Descripción del sistema
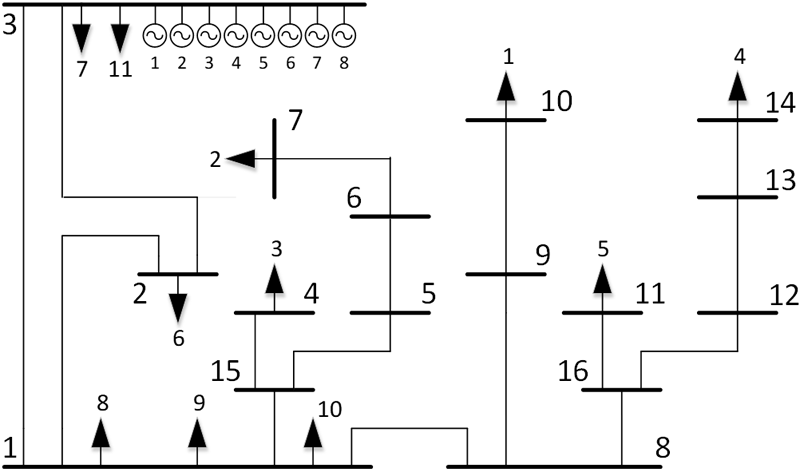
En la Fig. 2 se muestra el diagrama unifilar del Sistema EPU de 16 barras y 16 líneas de transmisión. Este modelo cuenta con 8 generadores convencionales existentes y con 11 puntos de demanda. Las características del sistema se detallan en la Tabla I y la Tabla II.
Únicamente las demandas dtj d de la 1 a la 6 son susceptibles de quedar completamente sin suministro. Las demandas restantes tienen enlaces adicionales de respaldo que pueden usar para no quedar sin servicio, sin embargo se consideran en el presente sistema ya que ésta es la configuración normal de operación. En ese sentido, durante la elaboración de los estados operativos Otj se ha tenido en cuenta que cuando la barra relacionada a una demanda con enlaces de respaldo queda fuera de servicio, dicha demanda también tenga el mismo estado –fuera de servicio– de forma tal que no se considere dentro del cálculo de racionamiento de demanda. Por lo tanto, el total de las demandas de la 1 a la 6 serán la base para el cálculo de los indicadores SAIFI y SAIDI.
Cada vez que la demanda total no suministrada cambia su valor de 0 a otra cantidad, un evento de interrupción es registrado. El final de este evento ocurre cuando el racionamiento vuelve a 0 otra vez. Para el cálculo del índice SAIDI se usa la suma del racionamiento total, mientras que para el SAIFI se considera únicamente la suma de los máximos racionamientos registrados dentro de cada evento. Se asume que todos los usuarios tienen cargas de iguales características.

Para la obtención del valor de la demanda para cada hora se hace uso de coeficientes escalados de un año típico que se multiplican al valor máximo de la demanda mostrada en la Tabla I. Estos coeficientes, sin embargo, no se muestran en esta comunicación por limitaciones de espacio. Así tampoco son mostradas las potencias que generan las centrales eólicas y solares para cada hora, las características de las líneas de transmisión, ni los estados operativos para los componentes del sistema.

Las posibles centrales RER identificadas para el Sistema EPU son en total 26, siendo conformadas por 13 granjas eólicas, 8 parques solares y 5 hidroeléctricas. Cada una de estas posibles centrales tiene por lo menos una línea de transmisión candidata asociada, existiendo en total 43 posibles circuitos a construir. Los datos de estas líneas también quedan fuera de esta comunicación por limitaciones de espacio.
Resultados obtenidos
Tres casos son analizados. El primer caso C01 representa la situación actual del Sistema EPU. El caso C02 evalúa los proyectos renovables y sus líneas de transmisión candidatas de una manera determinística. Finalmente, el caso C03 realiza un análisis estocástico de costo para seleccionar los mejores proyectos RER a ser implementados.
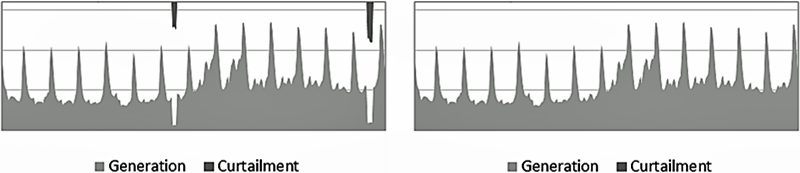
La Figura 3 muestra una pequeña serie de tiempo correspondiente a la operación del Sistema EPU bajo el caso C01 mientras la Figura 4 presenta las mismas horas bajo el caso C02. Resulta evidente la mejora en la calidad del servicio eléctrico pues en el caso C01 existe una fuerte presencia del racionamiento de la demanda sin embargo en el caso C02 ésta resulta casi imperceptible. Se debe aclarar que la falta de suministro para las demandas se debe prácticamente a fallas en las líneas de transmisión. Para el análisis de sensibilidad de costos (C03), las posibles variaciones mostradas en la Tabla III son usadas. Estos rangos indican las variaciones máximas y mínimas para los costos del proyecto. Existen en total 27 escenarios, teniendo cada uno una probabilidad de ocurrencia de 1/27.

De manera consiste con las tendencias de costos presentadas (International Energy Agency, 2016), la tecnología solar tiene el mayor rango de variación, seguido por la tecnología eólica. La tecnología hídrica se considera en una etapa madura por lo que se esperan muy pocos cambios en sus costos. El proceso de optimización debe encontrar el mix óptimo incluyendo estos posibles escenarios económicos.
Conclusiones
Los resultados mostrados en la Tabla IV indican que la implementación de centrales de generación distribuida en sistemas crítica mejoran notablemente la calidad y confiaibilidad del servicio eléctrico. Para el caso de estudio del Sistema EPU, se obtenien reducciones de aproximadamente el 90% en ambos indicadores SAIFI y SAIDI tanto para el caso C02 y C03.
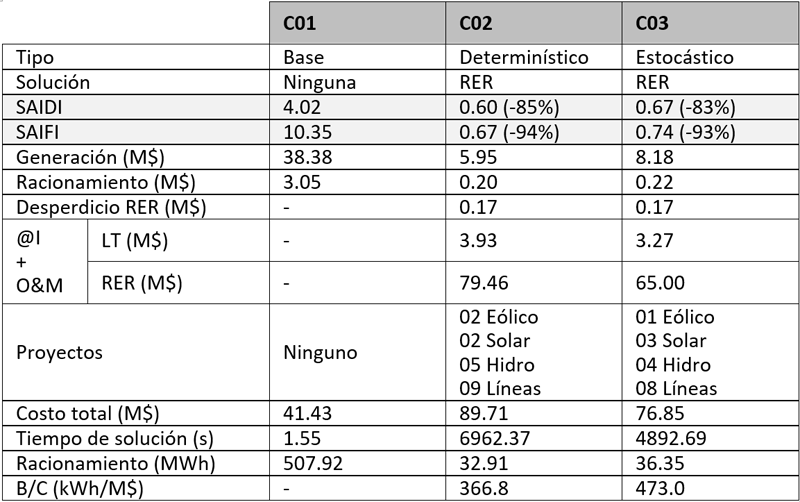
Los proyectos seleccionados inicialmente cambian luego de incluir el análisis estocástico de costos. Notese que en el caso C02, por ejemplo, fueron selecciondos 05 centrales hidroelectricas pero en el caso C03 esta cantidad se reduce al ser reemplazado uno de estos proyectos por una central solar. En efecto, este comportamiento es completamente lógico si se tiene en cuenta que la tecnología solar es la que más posibilidades tiene de reducir sus costos considerablemente en comparación con la tecnología hídrica que tiene un costo prácticamente fijo. Este análisis económico permite que el modelo elija una combinación de proyectos con una relación de Beneficio-Costo (B/C) superior, lo que sin duda contribuye a maximizar la eficiencia de las inversiones tanto públicas como privadas.
Para trabajos futuros, se recomienda analizar la implementación de sistemas de almacenamiento de energía como alternativa para conseguir valores de SAIFI y SAIDI mucho más cercanos a cero.
Referencias
Barbosa, J. et al, 2016, “Stochastic Generation and Transmission Planning Considering Future Renewable and Gas Opportunities in Queensland, Australia,” Power and Energy Society General Meeting (PESGM), USA.
International Energy Agency, 2016, World Energy Outlook 2016 [En línea]. Disponible en: https://goo.gl/ZdJBSj
Tang, L. et al, 2015, “Transmission System Planning Considering Integration of Renewable Energy Resources,” IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Australia.
Ugranli, F. & Karatepe, E., 2013, “Transmission Expansion Planning Considering Maximizing Penetration Level of Renewable Sources,” IEEE International Symposium on Innovation in Intelligent Systems and Applications (INISTA), Bulgaria.
Zheng, J. et al, 2015, “Transmission Planning with Renewable Generation and Energy Storage,” 10th International Conference on Advances in Power System Control, Operation & Management (APSCOM 2015), China.